In topology, a branch of mathematics, the Klein Bottle is an example of a non-orientable surface; it is a two-dimensional manifold against which a system for determining a normal vector cannot be consistently defined.
Informally, it is a one-sided surface which, if travelled upon, could be followed back to the point of origin while flipping the travelled upside down. Other related non-orientable objects include the Mobius strip and the real projective plane. While a Mobius strip is a surface with boundary, a Klien bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary.
The Klein Bottle was first described in 1882 by the german mathematician Felix Klein.
"If you glue The edges of two You get a weird bottle like mine." ~ Felix Klein
Body Shape
The parametrization of the 3-dimentional immersion of the bottle itself is much more complicated. Klein Bottle with slight transparency.

Dimensions
A true Klein Bottle lives in 4-dimensions. But every tiny patch of the Klein Bottle is 2-dimensional. In this sense, a Klein Bottle is a 2-dimensional manifold which can only exist in 4-dimensions!
Alas, our universe has only 3 spatial dimensions, so even Acme's dedicated engineers can't make a true Klein Bottle.
Construction
The following square is a fundamental polygon of the Klein bottle. The idea is to 'glue' together the corresponding red and blue edges with the arrows matching, as in the diagrams below. Note that this is an "abstract" gluing in the sense that trying to realize this in three dimensions results in a self-intersecting Klein bottle.
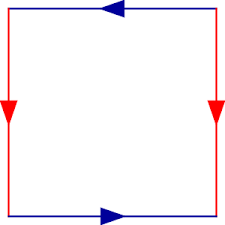
To construct the Klein bottle, glue the red arrows of the square together (left and right sides), resulting in a cylinder. To glue the ends of the cylinder together so that the arrows on the circles match, one would pass one end through the side of the cylinder. This creates a circle of self-intersection – this is an immersion of the Klein bottle in three dimensions.
